Find destination in geographical coordinates
gcDestination.RdFind the destination in geographical coordinates at distance dist and for the given bearing from the starting point given by lon and lat.
gcDestination(lon, lat, bearing, dist, dist.units = "km",
model = NULL, Vincenty = FALSE)Arguments
- lon
longitude (Eastings) in decimal degrees (either scalar or vector)
- lat
latitude (Northings) in decimal degrees (either scalar or vector)
- bearing
bearing from 0 to 360 degrees (either scalar or vector)
- dist
distance travelled (scalar)
- dist.units
units of distance "km" (kilometers), "nm" (nautical miles), "mi" (statute miles)
- model
choice of ellipsoid model ("WGS84", "GRS80", "Airy", "International", "Clarke", "GRS67"
- Vincenty
logical flag, default FALSE
Details
The bearing argument may be a vector when lon and lat are scalar, representing a single point.
Value
A matrix of decimal degree coordinates with Eastings in the first column and Northings in the second column.
References
http://www.movable-type.co.uk/scripts/latlong.html#ellipsoid,
the file earlier available at http:\/\/williams.best.vwh.net/avform.htm,
http://www.movable-type.co.uk/scripts/latlong-vincenty.html#direct,
Original reference https://www.ngs.noaa.gov/PUBS_LIB/inverse.pdf:
Vincenty, T. 1975. Direct and inverse solutions of geodesics on the ellipsoid with application of nested equations. Survey Review 22(176):88-93
See also
Examples
data(state)
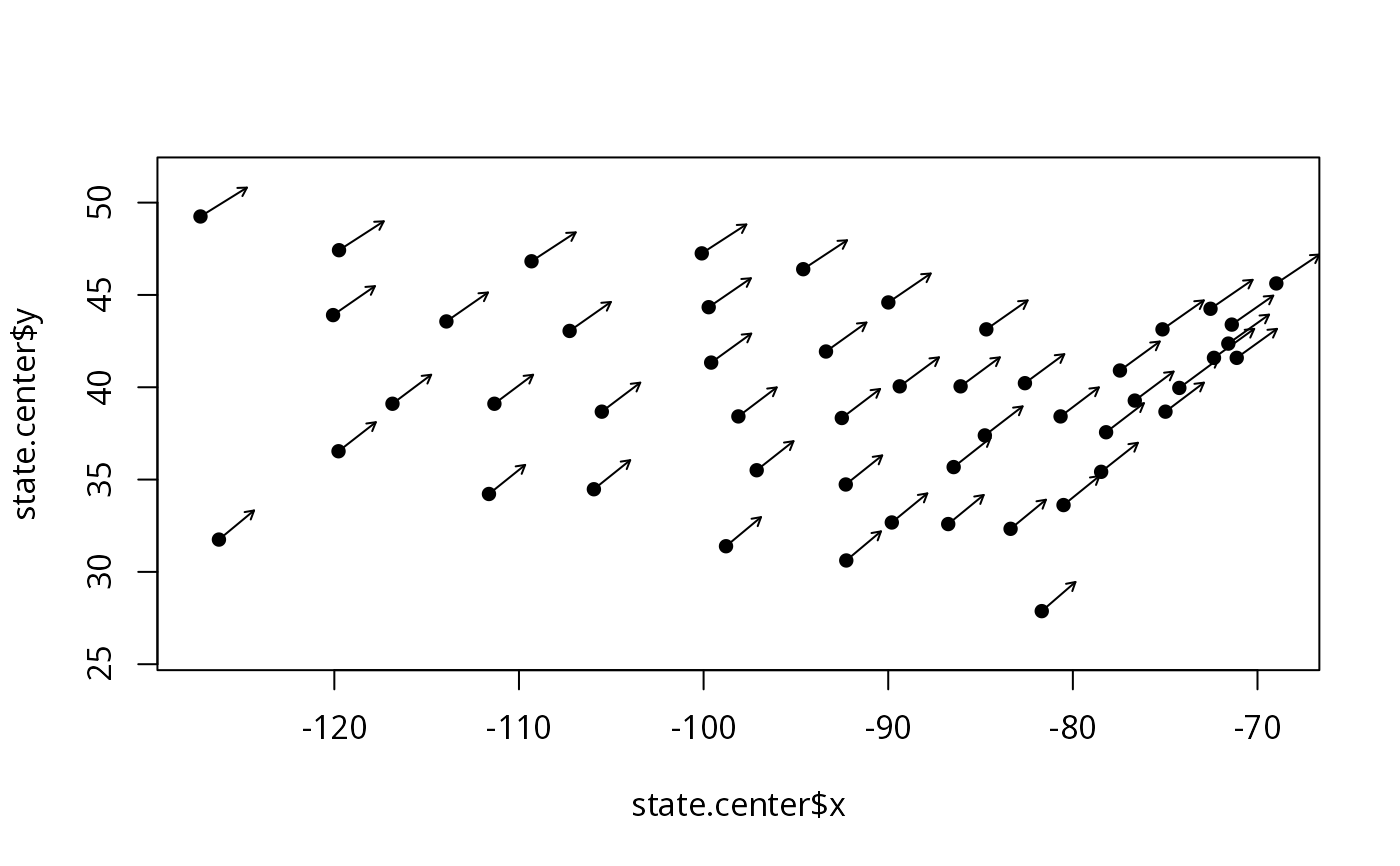
res <- gcDestination(state.center$x, state.center$y, 45, 250, "km")
plot(state.center$x, state.center$y, asp=1, pch=16)
arrows(state.center$x, state.center$y, res[,1], res[,2], length=0.05)
 llist <- vector(mode="list", length=length(state.center$x))
for (i in seq(along=llist)) llist[[i]] <- gcDestination(state.center$x[i],
state.center$y[i], seq(0, 360, 5), 250, "km")
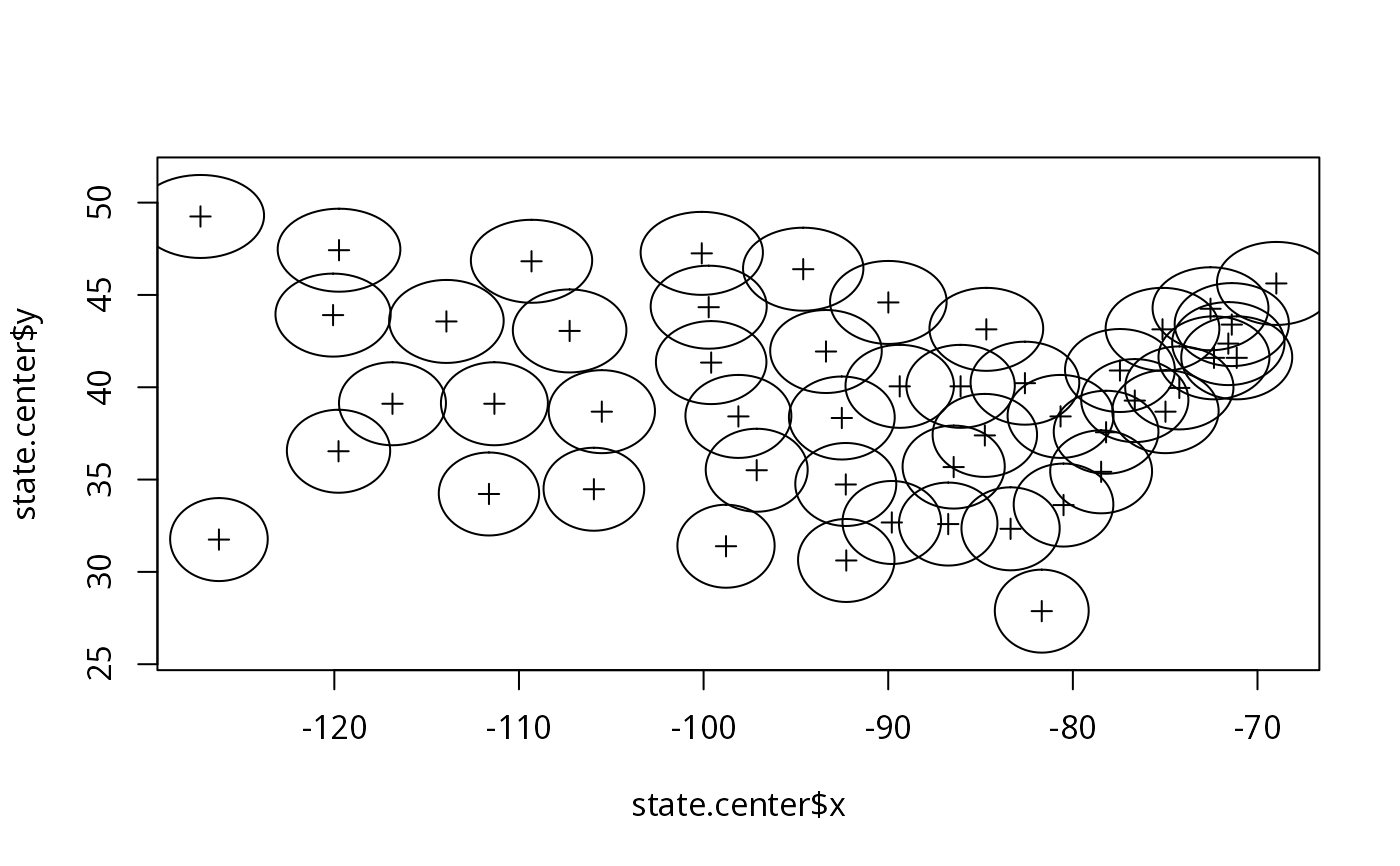
plot(state.center$x, state.center$y, asp=1, pch=3)
nll <- lapply(llist, lines)
llist <- vector(mode="list", length=length(state.center$x))
for (i in seq(along=llist)) llist[[i]] <- gcDestination(state.center$x[i],
state.center$y[i], seq(0, 360, 5), 250, "km")
plot(state.center$x, state.center$y, asp=1, pch=3)
nll <- lapply(llist, lines)